Value-Added with Quantitative Analysis
THE RHA REVIEW
Volume 7, No. 3, Second Quarter 2001
By Amy V. Puelz, Ph.D.
Starting with my receipt of a mathematics degree in the '80s, I have pursued the career path of a "quant," which I define as one who applies a variety of mathematical models to complex problems to structure, understand and possibly provide solutions. Over these past 20 years I can count on one hand the number of times a person, when finding out I consult, teach and research in statistics, mathematical modeling and simulation, does not respond with something to the effect of "I hate that stuff," "that was absolutely my worst class in college" or a more general "yuk." In defense of my chosen "quant" career path, I must attribute these visceral reactions to some memory trigger in the respondents' past, such as dropping a stack of computer punch cards on a windy day, memorizing statistical formulas with more Greek symbols than seen on campus during rush week, or some even-more-traumatizing numerical event. What I'd like to achieve in this column and several future columns is to convince you of the value of and relative ease with which quantitative analysis can be applied in risk- and insurance-related decision-making. In this column I'll focus on a firm's risk manager, and in future columns I'll explore the potential for quantitative analysis in insurance-related litigation support and insurance company operations.
The single-most-important reason for the growth in the application of quantitative analysis to risk- and insurance-related decision-making is the migration of analysis tools from the mainframe computers in the basement to executives' desks. Tools and techniques that were considered rocket science 20 years ago, from advanced statistical analysis to data mining, are now available in menu-driven, user-friendly packages on laptop computers. How can risk managers use these tools in decision-making? Two broad categories for potential application are the measure and quantification of risk, and the integration of the risk-management function.
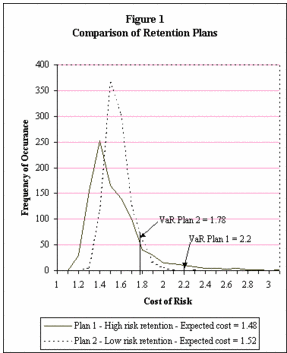
Measuring a firm's risk has received a lot of attention in recent years with the acceptance and implementation of Value at Risk (VaR) as the standard for reporting risk. VaR can be thought of as identifying the worst-case cost of risk. The academic and practitioner literature is now filled with tips, techniques and problems associated with the derivation and validity of a portfolio's VaR. At the very basic level, deriving VaR can be accomplished by using a simple computer spreadsheet package and generating random cost of risk outcomes, also called scenarios. These scenarios can be presented in a probability-distribution format similar to that in Figure 1, in which two risk-retention plans are compared — Plan 1 with high-risk retention (less insurance) and Plan 2 with low-risk retention (more insurance). Labeled for each plan is the VaR. In this case the VaR, or the worst-case cost of risk, is defined as the 95th percentile of risk costs. Plan 1, in which more risk is retained, has a higher VaR of 2.2 (compared with 1.78 for Plan 2) but has a lower expected cost of risk of 1.48 (compared with 1.52 for Plan 2). In other words, Plan 1, in which less insurance is purchased, is riskier but lower in cost. This worst-case or VaR analysis, in addition to the visual inspection of the probability distribution, can provide risk managers with valuable information when they are deciding how much and what type of insurance to purchase.
This process of comparing risk-retention plans becomes necessarily more complex when multiple risk and cash-flow streams are integrated into the analysis. This integrated view of a firm's risk is called enterprise risk management. A firm represents a complex arrangement of activities that are managed by functional and operational areas. Historically, the risk manager has focused attention on those events which hold the prospect of disrupting a firm's productivity without considering how loss events interact with profit-making events — in essence, the consideration of risk management and financial management within the same firm. The enterprise view of the firm is an approach that requires the identification of all the firm's important cash flows, not only those related to risk costs. All cash flows are then analyzed to determine how they change relative to other cash flows. Statistical techniques for measuring how a firm's risk and core business cash flows interact, such as correlation analysis, are available in standard spreadsheet packages; and others, such as principal component analysis, are available as add-ins for spreadsheets or operate in a stand-alone environment.
Once the relationships between the cash flows are established, random outcomes for all cash flows or scenarios are generated using simulation analysis. This process is similar to that described earlier in the VaR derivation, except that multiple cash flows representing important business risks and profit-making ventures are all generated for each scenario, capturing the interaction between all business functions and allowing for the development of an integrated firm-level decision methodology.
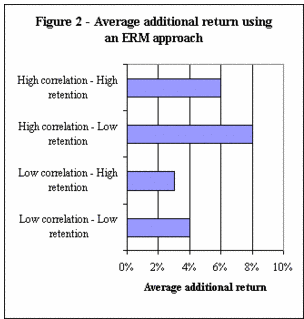
Figure 2 illustrates the savings realized using an ERM approach relative to a non-ERM approach. In this example a risk-related cash outflow and a profit-making cash inflow are generated, assuming either a high or low correlation between their movements. The ERM approach incorporates this interaction between cash flows in decision analysis, whereas the non-ERM approach views the cash flows in isolation, ignoring any interaction between them. The analysis was conducted assuming either a firm with a relatively high-risk retention in the form of a high per-loss deductible or one with a relatively low-risk retention. In this example, scenarios were generated for both the ERM and non-ERM assumptions, and an optimization decision model was executed on the PC to derive the optimal decision, given the possible set of cash-flow outcomes. The average additional return the firm realized using an integrated ERM approach is presented in Figure 2.
Both the VaR and ERM examples presented in this column used PC-based tools to provide managers with quantitative analysis to use in making better decisions regarding the management of a firm's risk. Careful development and use of models similar to these can be valuable for any risk manager. Quantitative analysis is no longer a report that comes from a black box in the basement but a dynamic, adaptable tool for managers to use in exploring alternatives for effective risk management.

